The following external R packages/functions are used:

library(dplyr)
library(ggplot2)
gather <- tidyr::gather

This note is a continuation from Dealing with a non-separable penalty term under 2018: Statistical Computation.

 

1. Introduction

This note concerns with a cross-validation method. In particular, it is interested in finding an optimal tuning parameter \(\lambda\) and a corresponding \(\boldsymbol{\theta}\) that yields a lowest cross-validation error. The note will demonstrate how the cross-validation is used to find \(\lambda\), and provide functions that help achieve the goal.

2. Choosing a tuning parameter

From the previous note, I assumed: \[y_t = \theta_t + \varepsilon_t\] with \(\varepsilon_t \stackrel{iid}{\sim} N(0, \sigma^2)\), and used the cost function that has a penalty: \[\text{cost}(\theta_1, \phi_2, \dots, \phi_n) = \sum_{t = 1}^{n} (y_t - \theta_t)^2 + \lambda \sum_{t = 2}^{n} |\phi_t|\] where \(\phi_t = \theta_t - \theta_{t - 1}\).

To find an optimal \(\lambda\), we shall use the following strategy:

  1. Divide \(y_t\)’s into \(k\) folds where the \(s\)th fold is defined as \(\text{Fold}_s := \{ y_{t} \}_{t \in A_s}\), where \(A_s = \{t \leq n \text{ | } t = s + kt^*, t^* \geq 0 \}\).
  2. Given \(\lambda\), compute the estimates \(\boldsymbol{\theta}_s\)’s based on \(\{y_t \}_{t \notin \text{Fold}_s}\) for all \(s = 1, \dots, k\).
  3. Define \(\text{interpolate}_{\boldsymbol{\theta}_s}(t)\) for each \(s\), an interpolating function based on \(\boldsymbol{\theta}_s\).
  4. Compute \(\text{loss}_s\) for each \(s\) where \[\text{loss}_s := \frac{1}{|\text{Fold}_s|} \sum_{t \in \text{Fold}_s} (\text{interpolate}_{\boldsymbol{\theta}_s}(t) - y_t)^2\]
  5. Compute \(\text{error} := \frac{1}{k}\sum_{s = 1}^{k} \text{loss}_s\).
  6. Choose \(\lambda\) that yields a minimum \(\text{error}\).

Step 1 is performed by split_data_1d:

Step 2 is performed by fusion_estimates, a function defined in the previous note:

Step 3 is done by interpolate_1d:

\(\text{loss}_s\) in step 4 is computed with loss_1d_fold:

and for the sake of computing training error, we define loss_1d as well:

We shall now compute the cross-validation error in cv_error_1d:

3. An example

The example in the previous note is regenerated:

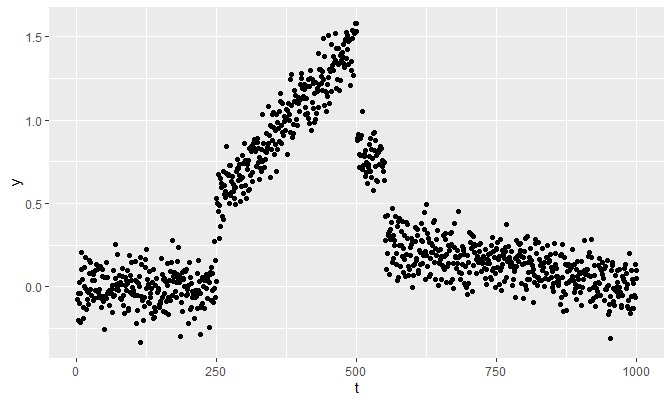
The following lambda values will be considered. Also, say \(k = 5\), an another arbitrary choice:

For each lambda, let’s compute the training error and the cross-validation error:

This process takes a while. Here’s the link to the errors csv file.

## Time difference of 34.66667 mins

The visualization is as follows:

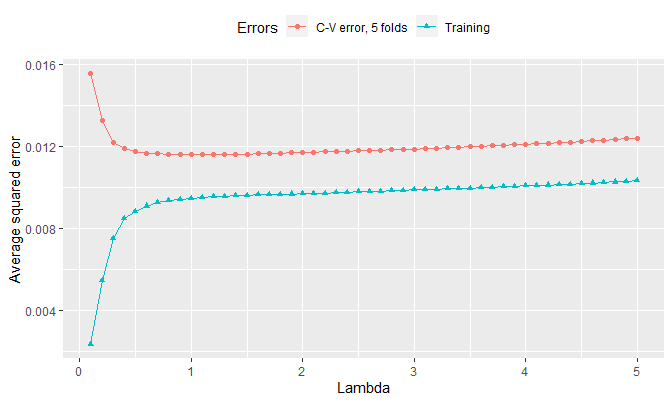
The training error increases as lambda increases. This makes sense since, as shown in the previous note, \(\theta_t \to \overline{y}\) for all \(t\) as \(\lambda\) gets greater, and \(\theta_t = \overline{y}\) for all \(t\) starting from a certain value of \(\lambda\). That is, as lambda increases, the fusion estimates start to move away from the least squares estimates \(\hat{\theta}_t\)’s (\(= y_t\) for all \(t\)), which are estimates when \(\lambda = 0\) and are values that minimize the average squared error, so the training error increases as shown in the plot.

The minimum lambda that yields the lowest cv-error is therefore:

## [1] 1

The proposed value of \(\lambda\) is 1.

Session info

R session info:

## R version 3.6.1 (2019-07-05)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 18362)
## 
## Matrix products: default
## 
## locale:
## [1] LC_COLLATE=English_Canada.1252 
## [2] LC_CTYPE=English_Canada.1252   
## [3] LC_MONETARY=English_Canada.1252
## [4] LC_NUMERIC=C                   
## [5] LC_TIME=English_Canada.1252    
## 
## attached base packages:
## [1] stats     graphics 
## [3] grDevices utils    
## [5] datasets  methods  
## [7] base     
## 
## other attached packages:
##  [1] ggConvexHull_0.1.0
##  [2] dplyr_0.8.3       
##  [3] reticulate_1.13   
##  [4] pROC_1.15.3       
##  [5] ggrepel_0.8.1     
##  [6] ggplot2_3.2.1     
##  [7] funpark_0.2.6     
##  [8] data.table_1.12.6 
##  [9] boot_1.3-22       
## [10] rmarkdown_1.17    
## [11] magrittr_1.5      
## [12] itertools2_0.1.1  
## 
## loaded via a namespace (and not attached):
##  [1] prettydoc_0.3.1 
##  [2] tidyselect_0.2.5
##  [3] xfun_0.11       
##  [4] purrr_0.3.3     
##  [5] lattice_0.20-38 
##  [6] colorspace_1.4-1
##  [7] vctrs_0.2.0     
##  [8] htmltools_0.4.0 
##  [9] yaml_2.2.0      
## [10] utf8_1.1.4      
## [11] rlang_0.4.2     
## [12] pillar_1.4.2    
## [13] glue_1.3.1      
## [14] withr_2.1.2     
## [15] lifecycle_0.1.0 
## [16] plyr_1.8.4      
## [17] stringr_1.4.0   
## [18] munsell_0.5.0   
## [19] gtable_0.3.0    
## [20] evaluate_0.14   
## [21] labeling_0.3    
## [22] knitr_1.26      
## [23] fansi_0.4.0     
## [24] Rcpp_1.0.3      
## [25] readr_1.3.1     
## [26] scales_1.1.0    
## [27] backports_1.1.5 
## [28] jsonlite_1.6    
## [29] farver_2.0.1    
## [30] png_0.1-7       
## [31] hms_0.5.2       
## [32] digest_0.6.23   
## [33] stringi_1.4.3   
## [34] grid_3.6.1      
## [35] cli_1.1.0       
## [36] tools_3.6.1     
## [37] lazyeval_0.2.2  
## [38] tibble_2.1.3    
## [39] crayon_1.3.4    
## [40] tidyr_1.0.0     
## [41] pkgconfig_2.0.3 
## [42] zeallot_0.1.0   
## [43] ellipsis_0.3.0  
## [44] Matrix_1.2-17   
## [45] xml2_1.2.2      
## [46] assertthat_0.2.1
## [47] rstudioapi_0.10 
## [48] iterators_1.0.12
## [49] R6_2.4.1        
## [50] compiler_3.6.1

Related page